前情提要

昨天已經把位置編碼的演進介紹完了，需要考慮的點蠻多的。

參考來源:
https://www.cnblogs.com/rossiXYZ/p/18744797
https://medium.com/thedeephub/positional-encoding-explained-a-deep-dive-into-transformer-pe-65cfe8cfe10b

1. 複習 & 觀念加強

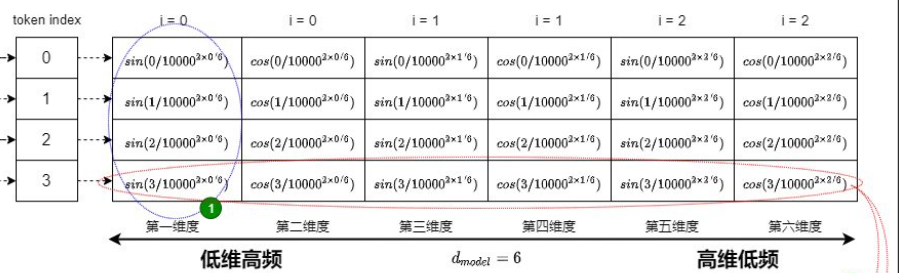
昨天有看過類似這張圖，這裡用底下這張圖講解。

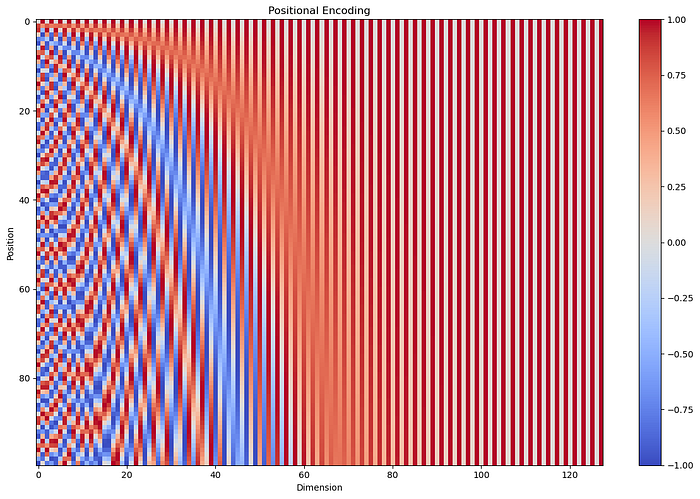
當中的圖不像昨天二進制一樣只有0, 1，他是一個連續的，透過以下幾個觀點來了解:

• X 軸: 位置編碼的不同維度，左邊低維，右邊高維
• Y 軸: 序列中第幾個 token
• 顏色: 數值範圍在 -1 到 1 之間（藍色接近 -1，紅色接近 1）。這是透過 sin 和 cos 函數生成的週期性數值。

觀念:

1. 想像左上角就像二進制的 0000
2. 向下走，顏色開始變化，類似二進制數字改變 (0000 → 0001)
3. 左邊低維 → 想像成二進制最後一個數字，每走一個就變化一次 → 快速震盪 → 提供短距離位置區分
4. 右邊高維 → 想像成二進制第四個數字，要經過很久才會改變一次 → 慢速震盪 → 提供長距離位置區分
   

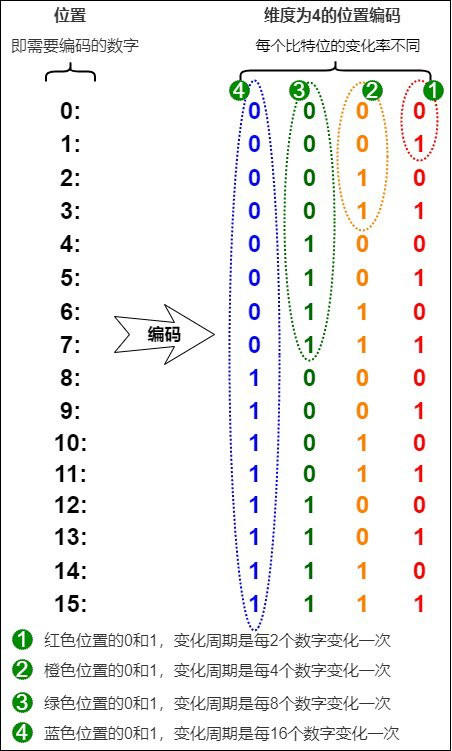
結論:
解決了昨天說的離散不連續的問題，值的範圍也有限，加上昨天說明過的，可以反應相對位置資訊。

2. 絕對位置編碼實作

這裡的實作只單做 positional encoding 這段，那整個是需要 token embedding 加起來才會得到最後的 word embedding。

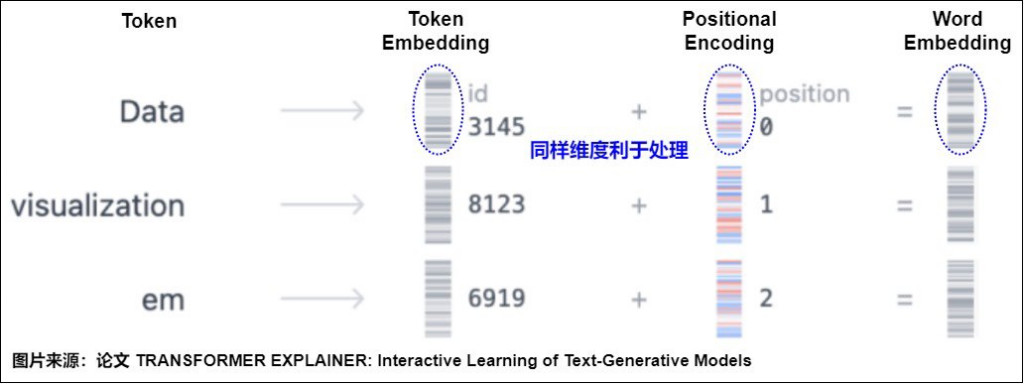
這裡我們先實作 pe 的部分，步驟如下:

1. 定義最基本的 class (init + forward) → 問自己 position_ids 輸入的維度是多少
2. 傳入 init 參數有 hidden_size, max_seq_len
3. 照昨天提到的公式寫一個 build_pos_enc，事先計算好如下圖二的表格，shape 為 (max_seq_len, hidden_size)，之後儲存起來，步驟如下:

1. 先宣告一個名稱為 pos_enc， shape 為 (max_seq_len, hidden_size) 全為 0 的表格 → 初始化的概念
2. 準備一個 position 像下圖 token index 一樣 → [0, 1, 2, …, max_seq_len -1] → 之後讓他 shape 變成 (L, 1) 用於後續相乘
3. 透過下圖一的公式先計算括號內的頻率 freq → 除 10000 的那個指數，記得兩個一組
4. 偶數位使用 sin, 奇數位使用 cos → 放到 pos_enc 表格當中，這裡會用到::運算
5. 儲存起來
   
   

4. 在 forward 準備要做計算
   輸入 position_ids 之後查事先準備好的表格就行

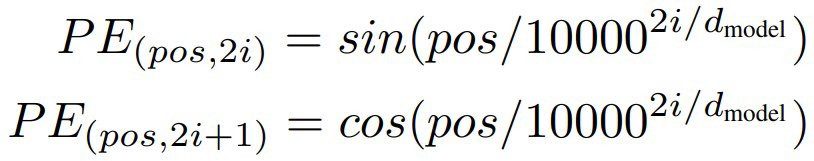
import torch
from torch import nn

# step1
class MyPositionEncoding(nn.Module):
    def __init__(self):
        super().__init__()

    def forward(self, position_ids: torch.Tensor):
        '''
            B: batch size
            L: seq len
            position_ids: (B, L)
        '''
        pass

# step2
class MyPositionEncoding(nn.Module):
    def __init__(self, max_seq_len, hidden_size):
        super().__init__()

        self.max_seq_len = max_seq_len
        self.hidden_size = hidden_size

    def forward(self, position_ids: torch.Tensor):
        '''
            B: batch size
            L: seq len
            position_ids: (B, L)
        '''
        pass

# step3 + step4 
class MyPositionEncoding(nn.Module):
    def __init__(self, max_seq_len, hidden_size):
        super().__init__()

        self.max_seq_len = max_seq_len
        self.hidden_size = hidden_size
        self.build_pos_enc()

    def build_pos_enc(self):
        # 初始化表格
        pos_enc = torch.zeros(self.max_seq_len, self.hidden_size)

        # 準備 position, shpae: L -> (L, 1) 用於等下相乘
        position = torch.arange(0, self.max_seq_len).unsqueeze(1)

        # inv 代表倒數的意思
        # 因為兩個一組，所以維度0, 1 會用同一個，所以 arange 一次加 2
        inv_freq = 1.0 / (10000 ** (torch.arange(0, self.hidden_size, 2).float() / self.hidden_size))
        # print((torch.arange(0, self.hidden_size, 2).float() / self.hidden_size))
        print(f'inv_freq: {inv_freq}')
        # print(position * inv_freq)

        # 偶數位使用 sin, 奇數位使用 cos → 放到 pos_enc 表格當中
        # 將等號右邊的 sin 算完，放到左邊取出偶數位置的表格上
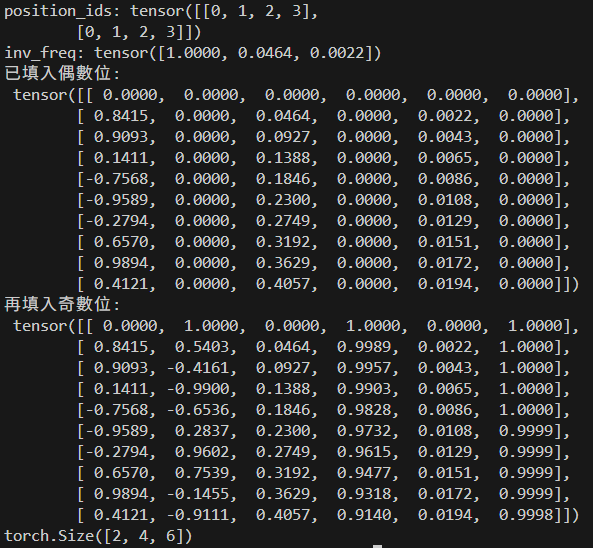
        pos_enc[:, 0::2] = torch.sin(position * inv_freq)
        print(f'已填入偶數位:\n {pos_enc}')

        pos_enc[:, 1::2] = torch.cos(position * inv_freq)
        print(f'再填入奇數位:\n {pos_enc}')

        # 儲存起來
        self.register_buffer('pos_enc', pos_enc)

    def forward(self, position_ids: torch.Tensor):
        '''
            B: batch size
            L: seq len
            position_ids: (B, L)
        '''
        return self.pos_enc[position_ids]
    
        # or 
        # return torch.embedding(self.pos_enc, position_ids)

測試程式

if __name__ == "__main__":

    B, L, D = 2, 4, 6
    x = torch.rand(B, L, D)
    start_pos = 0
    position_ids = torch.arange(
        start = start_pos, 
        end = start_pos + L, 
        dtype = torch.long
    ).unsqueeze(0).expand(B, -1)

    print(f'position_ids: {position_ids}')
    
    pe = MyPositionEncoding(
        max_seq_len = 10, 
        hidden_size = 6
    )

    y = pe(position_ids)
    print(y.shape)

一樣可以照著步驟試著想想看做做看，不過是真的沒想到分步驟花的時間真的久，希望可以幫到你更好了解，明天我們先換換口味，今天先到這囉~